Significación Estadística, ¿Ciencia o Pirotecnia?

Introducción
Ese momento de satisfacción al ver p < 0.05… ¿representa un descubrimiento genuino o es apenas un espejismo estadístico?
En la investigación científica, hay un instante que muchos anhelamos: después de meses de trabajo, ejecutamos el análisis y aparece p < 0.05. Sentimos alivio, validación. Creemos haber encontrado algo real, algo publicable.
Pero, ¿qué significa realmente ese número? ¿Y qué sucede cuando un ritual metodológico se convierte en el árbitro principal de la “verdad” científica?
Durante décadas, el umbral de significación estadística ha ocupado el lugar central en la investigación. Sin embargo, la evidencia acumulada y las reflexiones críticas —desde las advertencias de la American Statistical Association (ASA) en 2016 y 2019(Wasserstein and Lazar 2016; Wasserstein, Schirm, and Lazar 2019), hasta el llamado de más de 800 científicos en Nature(Amrhein, Greenland, and McShane 2019)— nos obligan a una conclusión incómoda: el problema no es solo cómo usamos el p-valor, sino el p-valor mismo.
Mi profesor Luis Carlos Silva Ayçaguer, pionero de esta crítica en Iberoamérica, lo planteó con claridad hace más de dos décadas: las pruebas de significación no necesitan ser reformadas —necesitan ser reemplazadas(Silva Ayçaguer 1997). No estamos ante un problema pedagógico, sino epistemológico.
Nota histórica: El ritual actual del NHST es una mezcla híbrida de dos tradiciones incompatibles: la de Ronald Fisher (quien propuso el valor p como medida continua de evidencia contra H₀) y la de Jerzy Neyman y Egon Pearson (quienes desarrollaron un marco de decisión con tasas de error fijas). Irónicamente, ninguno de los creadores aprobaría el uso mecánico que hacemos hoy(Greenland et al. 2016). El resultado es un híbrido conceptualmente incoherente que hemos convertido en dogma.
El Cohete: Cuando el Tamaño Muestral Fabrica “Verdades”
En la pirotecnia, un cohete más grande produce una explosión más fuerte. En estadística, ocurre algo perturbadoramente similar: el tamaño muestral actúa como nuestro “cohete”, capaz de fabricar “significación” donde no hay importancia.
Consideremos un ejemplo concreto: un ensayo clínico comparando dos tratamientos.
- Tratamiento nuevo: 51% de pacientes mejoran
- Tratamiento estándar: 49% de pacientes mejoran
- Diferencia absoluta: Solo 2 puntos porcentuales
¿Es esta diferencia clínicamente relevante? En la mayoría de contextos, claramente no. ¿Cambiaría la práctica médica? Difícilmente. ¿Justifica los costos y riesgos de cambiar de tratamiento? Casi nunca.
Pero observemos qué ocurre al aumentar el tamaño de muestra:
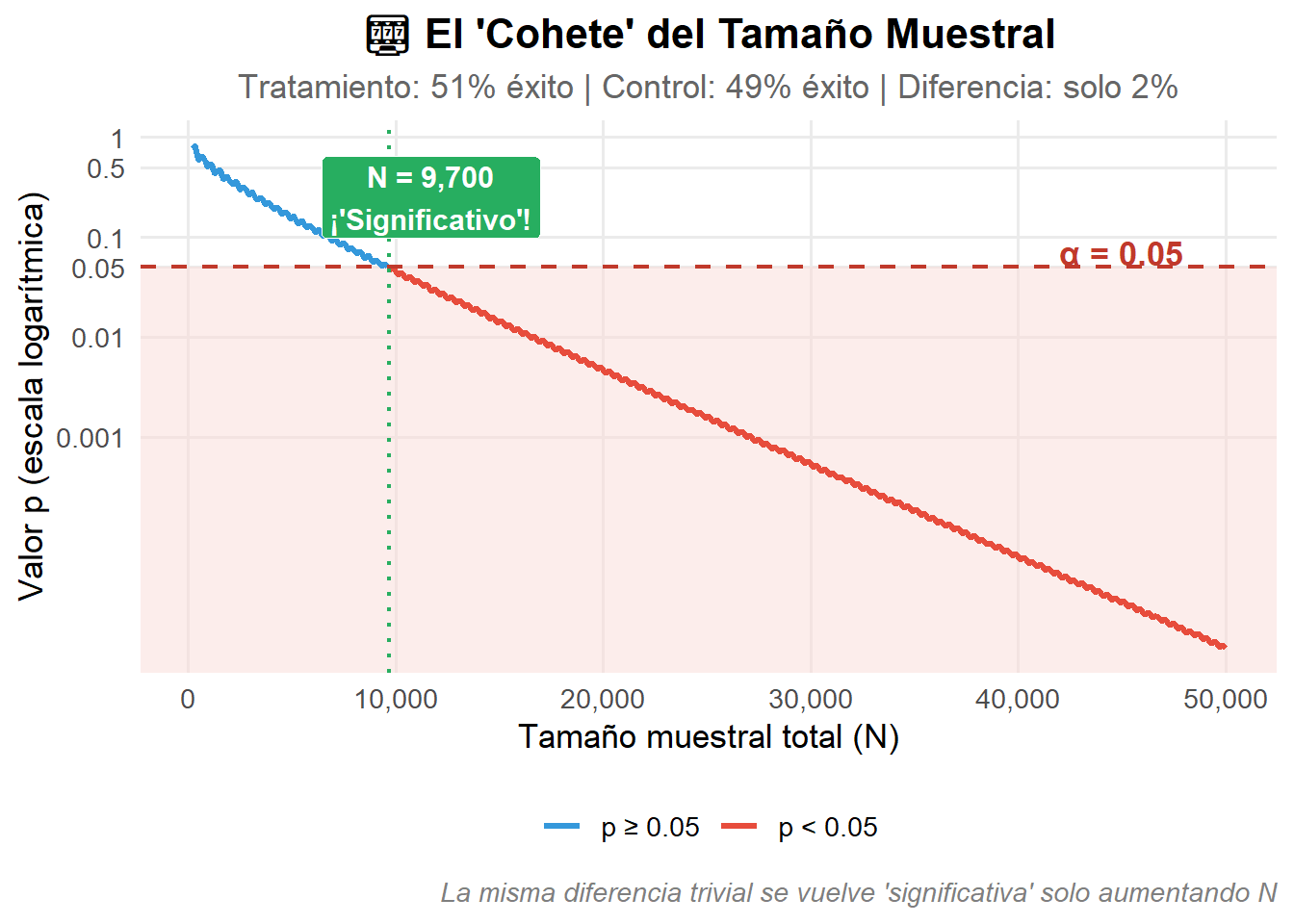
Este gráfico revela una verdad incómoda: la significación estadística es, en gran medida, una función del presupuesto de investigación. Con recursos suficientes para reclutar participantes, cualquier diferencia —por trivial que sea— puede cruzar el umbral mágico del p < 0.05.
La implicación es devastadora para la lógica del NHST: el p-valor no nos informa sobre la importancia del efecto, sino sobre la precisión de nuestra estimación (que depende de N). Estamos usando una herramienta que responde una pregunta que no hicimos.
La Explosión: Las Falacias del Valor p
El P-Valor Responde una Pregunta que Nadie Hace
La lógica del valor p es, en el mejor de los casos, contraintuitiva. Se calcula asumiendo que la hipótesis nula (H₀) es verdadera, y representa la probabilidad de observar datos tan extremos o más que los obtenidos, bajo ese supuesto.
Pero lo que queremos saber es completamente diferente:
| Lo que el p-valor MIDE | Lo que QUEREMOS saber |
|---|---|
| P(Datos extremos | H₀ verdadera) | ¿Cuál es la magnitud del efecto? |
| Probabilidad de datos dado H₀ | ¿Cuán precisa es la estimación? |
| Una probabilidad sobre DATOS | ¿Es relevante clínicamente? |
El p-valor responde: “Si no existiera ningún efecto, ¿cuán sorprendentes serían estos datos?”. Pero nosotros preguntamos: “¿Cuánto efecto hay y cuánto importa?”. Son preguntas radicalmente diferentes(Greenland et al. 2016).
La Falacia de la Transposición
El error más extendido es confundir P(Datos|H₀) con P(H₀|Datos). Confundirlas equivale a pensar que “la probabilidad de tener fiebre dado que tienes gripe” es igual a “la probabilidad de tener gripe dado que tienes fiebre”. Cualquier clínico sabe que son muy distintas.
La Ilusión de la Dicotomía
Un p = 0.049 y un p = 0.051 reciben tratamientos radicalmente diferentes en la literatura científica: uno es “significativo” (publicable, real, importante), el otro “no significativo” (descartable, nulo, irrelevante). Sin embargo, representan evidencia prácticamente idéntica(McShane et al. 2019).
Esta discontinuidad artificial no existe en la naturaleza. La hemos inventado nosotros, y distorsiona sistemáticamente el conocimiento científico.
El Caso del Chocolate: Anatomía del P-Hacking
En 2015, el periodista John Bohannon condujo un experimento revelador(Bohannon 2015). Realizó un pequeño ensayo aleatorizado sobre chocolate y pérdida de peso, midiendo 18 variables en muy pocos participantes.
El diseño garantizaba casi matemáticamente que alguna variable alcanzaría p < 0.05 por puro azar. Con 18 variables y α = 0.05, la probabilidad de al menos un “hallazgo significativo” por azar es aproximadamente:
P(al menos un falso positivo) = 1 − (1 − 0.05)^18 ≈ 0.60 (60%)
Es decir, 60% de probabilidad de “descubrir” algo inexistente.
Bohannon encontró su “resultado significativo” y los medios amplificaron la noticia: “¡El chocolate ayuda a perder peso!”. El estudio se publicó, se difundió globalmente, y demostró exactamente lo que pretendía: el sistema está roto.
El Veredicto: ¿Por Qué el NHST Es un Callejón Sin Salida?
Durante décadas, la defensa estándar del NHST ha sido: “el problema no son las pruebas de significación, sino su mal uso”. Esta defensa asume que existe un “buen uso” que podríamos alcanzar con mejor educación.
La evidencia sugiere lo contrario.
Sander Greenland y colaboradores documentaron 25 malinterpretaciones comunes del p-valor, y concluyeron que la interpretación correcta es “tan contraintuitiva que esperar su uso apropiado generalizado puede ser irrealista”(Greenland et al. 2016).
Gerd Gigerenzer fue más directo: el NHST es un “sustituto del pensamiento”, un ritual que reemplaza el razonamiento genuino por un procedimiento mecánico(Gigerenzer 2004).
John Ioannidis demostró que la mayoría de hallazgos publicados podrían ser falsos, en parte debido a la dependencia del sistema en el umbral arbitrario del p < 0.05(Ioannidis 2005).
Y Silva Ayçaguer planteó la cuestión fundamental: si después de décadas de educación estadística la comunidad científica sigue malinterpretando el p-valor, quizás el problema no sea la comunidad —quizás sea la herramienta(Silva Ayçaguer 1997).
Después del Humo: Alternativas Reales
Reconocer que el NHST es un callejón sin salida no significa abandonar la inferencia estadística. Significa transformarla.
De la Decisión a la Estimación
El cambio fundamental es pasar de preguntar “¿Es significativo?” a preguntar “¿Cuál es la magnitud del efecto y cuánta incertidumbre tenemos?”.
| Enfoque NHST (a abandonar) | Enfoque de Estimación (a adoptar) |
|---|---|
| “¿Es p < 0.05?” | “¿Cuál es el tamaño del efecto?” |
| Decisión binaria | Rango de valores compatibles |
| Umbral arbitrario | Relevancia clínica como criterio |
| Ritual mecánico | Razonamiento contextualizado |
Intervalos de Compatibilidad
Los mal llamados “intervalos de confianza” —mejor denominados intervalos de compatibilidad(Amrhein, Greenland, and McShane 2019)— nos muestran el rango de valores del parámetro que son razonablemente compatibles con los datos observados.
Interpretación correcta: Un intervalo del 95% significa que el procedimiento utilizado para construirlo capturará el verdadero parámetro en el 95% de las muestras a largo plazo. No significa que haya 95% de probabilidad de que el valor verdadero esté en este intervalo específico (eso requeriría un marco bayesiano).
Ventajas sobre el p-valor:
- Muestran la magnitud estimada del efecto
- Comunican la incertidumbre de la estimación
- Permiten evaluar relevancia práctica directamente
- No imponen dicotomías artificiales
El Enfoque Bayesiano
Los métodos bayesianos permiten responder la pregunta que realmente queremos hacer: “Dados estos datos, ¿cuán creíble es mi hipótesis?”.
Ventajas:
- Incorporan explícitamente el conocimiento previo
- Proporcionan probabilidades directas sobre hipótesis
- Se alinean con el razonamiento científico natural
- Permiten actualización continua del conocimiento
Consideraciones:
- Requieren especificar distribuciones prior
- La elección de priors debe ser transparente y justificada
- No son una “solución mágica” —tienen sus propias complejidades(McElreath 2020)
- Con priors poco informativas, suelen coincidir con resultados frecuentistas
Lo Que Realmente Necesitamos
Más allá de técnicas específicas, necesitamos un cambio cultural:
- Abandonar la dicotomía significativo/no significativo
- Reportar estimaciones con medidas de incertidumbre
- Contextualizar dentro del conocimiento previo
- Evaluar relevancia práctica, no solo estadística
- Ser transparentes sobre decisiones analíticas
- Pre-registrar estudios para evitar p-hacking
- Valorar la replicación tanto como el “descubrimiento”
Reflexión Final: Es Hora de Salir del Callejón
El debate sobre el valor p ha llegado a un punto de inflexión. En 2019, la American Statistical Association dio un paso sin precedentes al recomendar abandonar el término “estadísticamente significativo” por completo(Wasserstein, Schirm, and Lazar 2019). Más de 800 científicos respaldaron esta posición en Nature(Amrhein, Greenland, and McShane 2019).
Pero, ¿es suficiente abandonar el término mientras conservamos la práctica?
La respuesta, desde una perspectiva crítica, es no.
El p-valor no es simplemente una herramienta “mal usada”. Es una herramienta que:
- Responde una pregunta que nadie hace (probabilidad de datos extremos bajo H₀)
- Invita sistemáticamente a la malinterpretación (confusión con P(H₀|Datos))
- Impone dicotomías artificiales que no existen en la naturaleza
- Depende críticamente del tamaño muestral, no de la importancia del efecto
- Ha resistido décadas de esfuerzos educativos sin mejorar su uso
Si después de 70 años de educación estadística la comunidad científica sigue malinterpretando el p-valor, el problema no es la comunidad. El problema es la herramienta.
La invitación no es a “usar mejor” los p-valores —esa esperanza ha demostrado ser una ilusión—, sino a liberarnos de ellos:
- Estimar en lugar de decidir: Reportar magnitudes con intervalos de compatibilidad
- Contextualizar en lugar de automatizar: Situar los resultados en el conocimiento previo
- Razonar en lugar de ritualizar: Evaluar relevancia práctica, no umbrales arbitrarios
- Aceptar la incertidumbre: Reconocer que ningún número mágico puede dictar la “verdad”
La ciencia no avanza mediante rituales que sustituyen el pensamiento. Avanza cuando nos atrevemos a razonar, a contextualizar, y a reconocer los límites de nuestras herramientas.
Es hora de dejar atrás el callejón sin salida.
¡Tu Turno!
¿Has experimentado la presión del “p < 0.05” en tu campo? ¿Has visto cómo distorsiona las decisiones de investigación? ¿Qué alternativas has encontrado útiles?
Comparte tu experiencia en los comentarios. La transformación de la práctica científica comienza con conversaciones honestas.
Referencias
Amrhein, Valentin, Sander Greenland, and Blake McShane. 2019. “Scientists Rise up Against Statistical Significance.” Nature 567 (7748): 305–7. https://doi.org/10.1038/d41586-019-00857-9.
Bohannon, John. 2015. “I Fooled Millions into Thinking Chocolate Helps Weight Loss. Here’s How.” https://gizmodo.com/i-fooled-millions-into-thinking-chocolate-helps-weight-1707251800.
Gigerenzer, Gerd. 2004. “Mindless Statistics.” The Journal of Socio-Economics 33 (5): 587–606. https://doi.org/10.1016/j.socec.2004.09.033.
Greenland, Sander, Stephen J. Senn, Kenneth J. Rothman, John B. Carlin, Charles Poole, Steven N. Goodman, and Douglas G. Altman. 2016. “Statistical Tests, p Values, Confidence Intervals, and Power: A Guide to Misinterpretations.” European Journal of Epidemiology 31 (4): 337–50. https://doi.org/10.1007/s10654-016-0149-3.
Ioannidis, John P. A. 2005. “Why Most Published Research Findings Are False.” PLoS Medicine 2 (8): e124. https://doi.org/10.1371/journal.pmed.0020124.
McElreath, Richard. 2020. Statistical Rethinking: A Bayesian Course with Examples in r and Stan. 2nd ed. Boca Raton: CRC Press.
McShane, Blakeley B., David Gal, Andrew Gelman, Christian Robert, and Jennifer L. Tackett. 2019. “Abandon Statistical Significance.” The American Statistician 73 (sup1): 235–45. https://doi.org/10.1080/00031305.2018.1527253.
Silva Ayçaguer, Luis Carlos. 1997. “Las Pruebas de Significación Estadística En Tres Revistas Biomédicas: Una Revisión Crítica.” Revista Panamericana de Salud Pública 1 (5): 300–306. https://doi.org/10.1590/S1020-49891997000500001.
Wasserstein, Ronald L., and Nicole A. Lazar. 2016. “The ASA Statement on p-Values: Context, Process, and Purpose.” The American Statistician 70 (2): 129–33. https://doi.org/10.1080/00031305.2016.1154108.
Wasserstein, Ronald L., Allen L. Schirm, and Nicole A. Lazar. 2019. “Moving to a World Beyond p < 0.05.” The American Statistician 73 (sup1): 1–19. https://doi.org/10.1080/00031305.2019.1583913.