Gran Concurso: Miéntenle a su Profesor

El momento en que supieron que habían perdido
A las 11:07 de la mañana, aula de postgrado de la Universidad de Ciencias Médicas de la Habana , La Confiada dejó caer el bolígrafo.
En la pantalla del proyector, el histograma de sus datos mostraba un patrón inusual. Sus valores de hemoglobina —42 números cuidadosamente inventados usando su conocimiento de fisiología— acababan de ser expuestos como falsos.
Junto a ella, La Prudente miraba su propio veredicto: una varianza inexplicable.
La Entusiasta, que había escrito 47 valores en 60 segundos apostando por la cantidad sobre la calidad, tenía la expresión de quien acaba de descubrir que su estrategia era la menos mala.
Todo había comenzado media hora antes con una instrucción simple:
Tienen 60 segundos. Escriban todos los valores de hemoglobina en sangre de mujeres adultas que puedan inventar. Sin referencias. Sin calculadora. El que engañe mejor a las pruebas estadísticas, gana.
Lo que no sabían es que los humanos somos terribles inventado datos.
No porque seamos honestos, sino porque nuestro cerebro tiene bugs predecibles.
Y yo tenía exactamente las herramientas para encontrarlos.
Los sospechosos
Antes de la autopsia, conozcamos a nuestros participantes, médicos residentes que cursaban la asignatura de “Metodología de la investigación y estadística” en el curso 2022-2023 en la Universidad de Ciencias Médicas de la Habana (UCMH):
| Participante | Estrategia Declarada |
|---|---|
| Luidmila (La Prudente) | “Voy a quedarme en el rango seguro, nada muy extremo.” |
| Betsy (La Entusiasta) | “Voy a escribir muchos números para que parezca más real y ganar por cantidad de valores.” |
| Melissa (La Confiada) | “Sé fisiología. Esto va a ser fácil.” |
La escena del crimen: Mucha sangre o al menos uno de sus componentes, la Hemoglobina
Para que una mentira sea creíble, hay que conocer la verdad:
| Parámetro | Valor real |
|---|---|
| Variable | Concentración de hemoglobina en sangre (mujer adulta) |
| Unidad | g/L |
| Rango normal | 121 – 151 g/L |
| Media poblacional | 136 g/L |
| Desviación estándar | 7.5 g/L |
Armadas con este conocimiento (o su vaga memoria de él), las participantes escribieron furiosamente durante 60 segundos en su fichero de Excel todos las cifras que pudieron.
El resultado: 127 valores inventados listos para el análisis forense.
Acto II: La autopsia estadística
Primera prueba: ¿Acertaron el centro?
Empecemos por lo fácil. ¿La media aritmética del conjunto de datos inventados se parecen al valor real?
| Participante | Valores inventados | Media aritmética | Error de estimación | Resultado |
|---|---|---|---|---|
| La Entusiasta | 47 | 133.3 | -2.7 | Aceptable |
| La Prudente | 38 | 134.8 | -1.2 | ✓ Muy buena |
| La Confiada | 42 | 136.0 | 0.0 | ✓ Excelente |
Todas lograron estimaciones clínicamente válidas - los errores están dentro del margen aceptable en práctica médica:
- Variación biológica normal: 2-3 g/L
- Error de medición típico: 1-2 g/L
- Umbral de relevancia clínica: >5 g/L
En contexto real, estas diferencias no alterarían decisiones diagnósticas ni terapéuticas.
Intuir el centro de una distribución es relativamente fácil. Nuestro cerebro es bueno encontrando promedios.
Pero aquí viene el problema…
Segunda prueba: ¿Simularon bien la variabilidad?
Como médicos, nuestros participantes tienen experiencia clínica que les permitió estimar bien la tendencia central de los datos. Pero un desafío mayor aparece al intentar reproducir la dispersión. La variabilidad resulta mucho más difícil de intuir que el promedio. Veamos qué sucedió:
| Participante | Desviación Estándar | Minimo | Maximo | Error Absoluto | Error Relativo (%) | Resultado |
|---|---|---|---|---|---|---|
| La Confiada | 8.5 | 119 | 148 | 1.0 | 13.3 | Adecuada |
| La Entusiasta | 15.1 | 108 | 156 | 7.6 | 101.3 | Muy alta |
| La Prudente | 4.1 | 127 | 141 | 3.4 | 45.3 | Muy alta |
Error absoluto: Cuánto nos equivocamos con respeto al parámetro poblacional (Ejemplo: |8.5 - 7.5| = 1.0 g/L).
Error relativo: Qué porcentaje del valor real representa nuestro error (Ejemplo: |(8.5 - 7.5)/7.5| × 100% = 13.3%).
Hallazgo 1: Nadie acertó la variabilidad.
- La Prudente fue demasiado conservadora (rango 127-141)
- La Entusiasta fue demasiado caótica (rango 108-156)
- La Confiada se acercó bastante.
¿Por qué? Porque la variabilidad real es incómoda. Incluye valores que “no se ven bien”: una hemoglobina de 119 o de 153 parece “rara”, aunque sea perfectamente posible.
El cerebro humano evita lo incómodo. La naturaleza no.
Tercera prueba: El último dígito
Esta es mi prueba favorita. Simple, brutal, casi imposible de engañar.
La lógica: Imaginen una bolsa opaca con 10 fichas numeradas del 0 al 9. Si meten la mano y sacan una ficha al azar (y luego la devuelven), cada número tiene exactamente la misma probabilidad de salir: un 10%.
En datos clínicos reales, el último dígito de una medición precisa se comporta igual que esas fichas: es puro ruido aleatorio.
Pero el cerebro humano no funciona como el azar; funciona buscando comodidades.
Veamos qué hicieron nuestras residentes. En la siguiente tabla, he resaltado en negrita los valores que se desvían sospechosamente de ese 10% esperado:
| Dígito | La Confiada | La Entusiasta | La Prudente |
|---|---|---|---|
| 0 | 23.8% | 23.4% | 28.9% |
| 1 | 4.8% | 8.5% | 7.9% |
| 2 | 4.8% | 4.3% | 2.6% |
| 3 | 4.8% | 8.5% | 2.6% |
| 4 | 14.3% | 4.3% | 5.3% |
| 5 | 14.3% | 21.3% | 15.8% |
| 6 | 7.1% | 4.3% | 10.5% |
| 7 | 11.9% | 10.6% | 5.3% |
| 8 | 4.8% | 6.4% | 7.9% |
| 9 | 9.5% | 8.5% | 13.2% |
¿Lo notan? Es difícil ver el patrón solo con números. Hagámoslo visible.
En este gráfico, he pintado de rojo cualquier barra que supere la línea del azar (10%). Observen dónde se concentran las alertas:
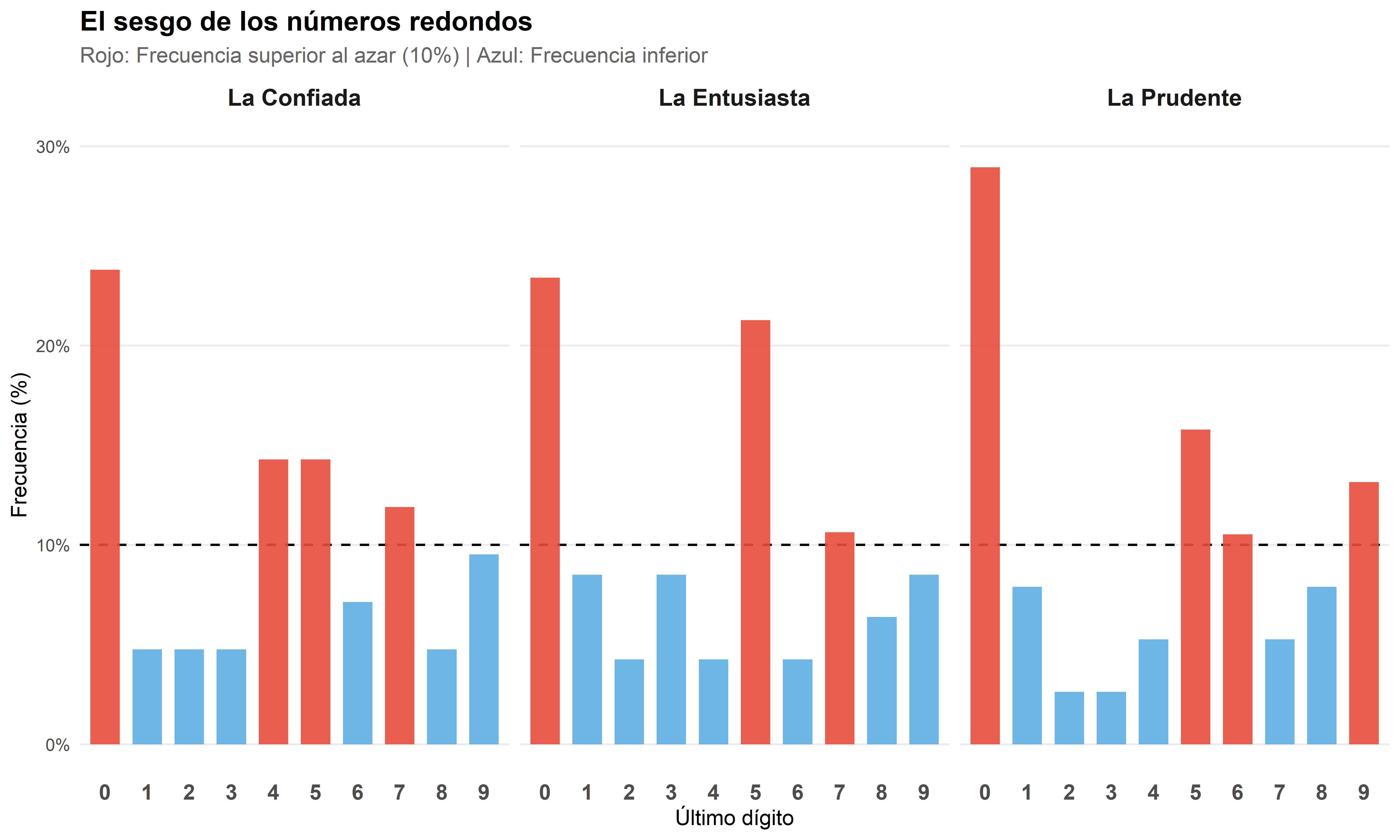
El patrón del mentiroso emerge:
- 🚨 El 0 y el 5 dominan (números “redondos”)
- 🚨 El 3, 7 y 9 casi desaparecen (números “incómodos”)
Para ser justos, el azar nunca es perfecto. ¿Cómo distinguimos el ruido natural del fraude?
En lugar de usar pruebas de significación complejas, usaremos una métrica descriptiva más honesta: la Desviación Promedio.
La pregunta es simple: “En promedio, ¿cuántos puntos porcentuales se equivocó la alumna en cada dígito respecto al 10% ideal?”
- 0% - 2%: Ruido natural (Aleatorio).
- 2% - 4%: Zona gris (Sospechoso).
- 4%: Sesgo sistemático (Artificial).
| Participante | Desviación Promedio | Peor Error |
|---|---|---|
| La Prudente | 5.7 % | 18.9 % |
| La Entusiasta | 5.1 % | 13.4 % |
| La Confiada | 4.9 % | 13.8 % |
La Prudente se desvió, en promedio, un 4.4% en cada dígito. Su “peor error” fue poner casi un 24% de ceros (un exceso de 14 puntos). Eso no es mala suerte; es un sesgo cognitivo masivo.
¿Por qué funciona esto?
Tu cerebro es una máquina de ahorrar energía. En 60 segundos, calcular “137” o “129” cuesta milisegundos valiosos. Escribir “130” o “135” es casi automático.
Bajo presión, la comodidad cognitiva vence a la creatividad estadística.
Profe, ¿por qué el último dígito es Uniforme (10% cada uno) y no sigue la Ley de Benford? (clic para ver la respuesta)
Porque los primeros números obedecen a la Homeostasis, pero el último obedece al caos.
Piensen en una Hemoglobina de 136 g/L:
- Los primeros dígitos (13-): Son obra de la Médula Ósea. Dependen de la eritropoyetina, el hierro y semanas de maduración celular. Son estructuras biológicas rígidas y lentas (Siguen leyes como Benford).
- El último dígito (-6): Es obra de un Vaso de Agua o otro factor. Depende de si el paciente sudó, si tomó café o si la máquina del laboratorio vibró. Es puro ruido transitorio.
La biología define el 130; el azar decide si es 136, 135 o 137.
Cuarta prueba: La aversión a la repetición
Otro bug del cerebro humano: odiamos repetirnos.
Si escribes “134” y luego tienes que escribir otro número, tu cerebro grita: "¡No pongas 134 otra vez! ¡Se verá falso!"
Pero en datos reales, las repeticiones son normales.
Imaginen el modo “Aleatorio” (Shuffle) de Spotify. Originalmente era puro azar, pero los usuarios se quejaban si salían dos canciones seguidas del mismo artista. Spotify tuvo que trucar el algoritmo para hacerlo menos aleatorio (evitando repeticiones) y que así pareciera más aleatorio a los humanos.
En medicina, un corazón sano tiene variabilidad (caos). Un corazón que late como un metrónomo (arriba, abajo, arriba, abajo) es patológico. Al inventar datos, el humano suele actuar como ese metrónomo, alternando valores altos y bajos para “equilibrar” la media.
Veamos si nuestras residentes cayeron en la trampa:
| Participante | Índice Z | Diagnóstico | Veredicto |
|---|---|---|---|
| La Confiada | 0.00 | Aleatoriedad perfecta | Aleatoriedad normal ✓ |
| La Entusiasta | -0.44 | Agrupamiento excesivo | Aleatoriedad normal ✓ |
| La Prudente | -0.60 | Agrupamiento excesivo | Aleatoriedad normal ✓ |
¡Sorpresa! Aquí la intuición nos falló.
Contra todo pronóstico, las tres residentes pasaron esta prueba.
-
La Confiada obtuvo un Z de 0.00. Una aleatoriedad matemática perfecta (casi demasiado perfecta, irónicamente).
-
La Prudente y La Entusiasta mostraron un ligero agrupamiento, pero totalmente dentro del rango de lo posible.
Lección Forense Vital: Este resultado demuestra por qué nunca debes confiar en una sola prueba estadística.
Si solo hubiéramos usado el Test de Rachas, habríamos concluido que los datos eran reales. Pero como vimos en la Prueba del Último Dígito, sabemos que son falsos.
El mentiroso puede tener suerte con la secuencia (arriba/abajo), pero es mucho más difícil que controle la micro-estructura de los números (dígitos finales). Por eso necesitamos una batería de pruebas, no una sola bala de plata.
Quinta prueba: El fantasma de Benford
La Ley de Benford es el detector de mentiras favorito de auditores y estadísticos forenses.
Normalmente, el primer dígito sigue una curva logarítmica (el 1 aparece el 30% de las veces). Pero la hemoglobina de una mujer adulta sana casi siempre empieza por 1 (Rango 120-150). Aquí Benford parece inútil… a menos que miremos bajo el capó.
El Truco: La Ley de Benford generalizada nos dice que el patrón logarítmico se mantiene en el Segundo Dígito, aunque es más sutil.
- El 1 (ej. 110, 115) debe ser más frecuente que el 2 (120, 125).
- El 2 más que el 3, y así sucesivamente.
Veamos si las residentes respetaron esta geometría natural o impusieron su propia voluntad:
| Participante | Conformidad |
|---|---|
| La Confiada | No conforme con Benford 🚨 | |
| La Entusiasta | Desviación moderada ⚠️ |
| La Prudente | No conforme con Benford 🚨 | |
El Patrón del Fracaso: ¿Por qué fallaron estrepitosamente?
Para cumplir la Ley de Benford en el segundo dígito, tendrían que haber generado muchos valores bajos (120-129) y menos valores altos (140-149).
Pero recordemos la Estrategia de La Prudente: “Quedarse en el rango seguro”. Al tener miedo a los extremos (120 o 150), concentraron casi todos sus datos en el “centro cómodo” (130-139).
Esto infló artificialmente el segundo dígito 3. Y mató los dígitos 2 y 4.
Interludio: La Caja de Herramientas del Detective Estadístico
Las técnicas que usamos en este “concurso” no son un juego. Son las mismas que utilizan auditores, comités de integridad científica y estadísticos forenses para detectar datos fabricados.
Aquí presento siete herramientas para analizar una sola variable numérica en busca de anomalías.
Herramienta 1: Análisis del Último Dígito
Principio: En datos naturales, el último dígito (0-9) debería distribuirse de forma aproximadamente uniforme (~10% cada uno).
Qué detecta:
- Preferencia por números “redondos” (0, 5) - Aversión a dígitos “incómodos” (3, 7, 9) - Redondeo excesivo
Test estadístico: Chi-cuadrado de bondad de ajuste contra distribución uniforme.
Interpretación:
| p-valor | Interpretación |
|---|---|
| > 0.10 | Compatible con datos reales |
| 0.05 - 0.10 | Zona gris, investigar más |
| < 0.05 | Evidencia de no uniformidad |
| < 0.01 | Fuerte evidencia de anomalía |
Limitaciones:
- Algunas variables tienen último dígito no uniforme por naturaleza\
- Instrumentos de medición pueden introducir sesgos legítimos
Referencia: Mosimann, J. E., et al. (1995). “Terminal digits and the examination of questioned data.” Chance, 8(2), 23-27.
Herramienta 2: Ley de Benford
Principio: En muchos datasets naturales, el primer dígito significativo NO es uniforme. El 1 aparece ~30% de las veces, decreciendo logarítmicamente.
Fórmula:
\(P(d) = \log_{10}\left(1 + \frac{1}{d}\right)\)
Distribución esperada:
| Dígito | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| % | 30.1% | 17.6% | 12.5% | 9.7% | 7.9% | 6.7% | 5.8% | 5.1% | 4.6% |
Qué detecta:
- Datos inventados (los humanos asumen uniformidad)
- Manipulación de cifras
- Duplicación de registros
Cuándo NO aplicar:
- Datos con rango restringido (usar segundo dígito)
- Números asignados (DNI, códigos)
- Datos truncados por diseño
Referencia: Benford, F. (1938). “The Law of Anomalous Numbers.” Proceedings of the American Philosophical Society, 78(4), 551-572.
Herramienta 3: Test de Rachas (Runs Test)
Principio: En una secuencia aleatoria, los valores por encima y por debajo de la mediana deberían alternarse de forma impredecible.
Qué detecta:
- Alternancia excesiva (el humano evita repetir)
- Agrupamiento excesivo (copiar-pegar)
- Patrones cíclicos ocultos
Interpretación:
- Demasiadas rachas → alternancia artificial
- Muy pocas rachas → agrupamiento sospechoso
Herramienta 4: Análisis de Duplicados
Principio: En datos reales, cierto nivel de repetición es esperado y depende del tamaño muestral y la precisión del instrumento.
Qué detecta:
- Ausencia sospechosa de repeticiones
- Exceso de valores idénticos
- Patrones de repetición no aleatorios
Ejemplo: En 50 valores de hemoglobina (rango ~30 valores posibles), esperaríamos 20-40% de repeticiones. Si hay 0%, es sospechoso.
Referencia: Carlisle, J. B. (2017). “Data fabrication and other reasons for non-random sampling in 5087 randomised, controlled trials.” Anaesthesia, 72(8), 944-952.
Herramienta 5: GRIM Test
Principio: Dados un tamaño muestral (n) y una escala de medición, solo ciertas medias son matemáticamente posibles.
Ejemplo: Si tienes n=20 valores enteros, la media debe ser un múltiplo de 0.05. Una media reportada de 7.32 es imposible.
Qué detecta:
- Medias fabricadas sin datos de respaldo\
- Errores de transcripción\
- Inconsistencias entre estadísticos reportados
Referencia: Brown, N. J. L., & Heathers, J. A. J. (2017). “The GRIM Test.” Social Psychological and Personality Science, 8(4), 363-369.
Herramienta 6: SPRITE
Principio: Dado un conjunto de estadísticos reportados (media, DS, n, rango), reconstruir todos los datasets posibles. Si ninguno tiene sentido, los estadísticos son sospechosos.
Qué detecta:
- Combinaciones imposibles de estadísticos\
- Datos que “no pueden existir”
Referencia: Heathers, J. A. J., & Brown, N. J. L. (2019). “SPRITE: A simple procedure for retrieving and installing true experimental data.” PsyArXiv.
Herramienta 7: Análisis de Distribución
Principio: Los datos inventados tienden a ser “demasiado normales” o “demasiado uniformes”. La realidad es más desordenada.
Métricas clave:
| Medida | Qué mide | Valor típico |
|---|---|---|
| Asimetría | Desbalance izq/der | 0 |
| Curtosis | Peso de las colas | 3 |
Análisis de Distribución: (Clic para ver las pruebas)

Referencia:
Simonsohn, U. (2013). “Just Post It.” Psychological Science, 24(10),
1875-1888.
Resumen: Matriz de Herramientas
| Herramienta | Pregunta clave | Dificultad |
|---|---|---|
| Último dígito | ¿Dígitos finales uniformes? | ⭐ |
| Benford | ¿Primeros dígitos naturales? | ⭐ |
| Runs test | ¿Secuencia aleatoria? | ⭐⭐ |
| Duplicados | ¿Repetición plausible? | ⭐ |
| GRIM | ¿Media posible? | ⭐⭐ |
| SPRITE | ¿Dataset posible? | ⭐⭐⭐ |
| Distribución | ¿Forma natural? | ⭐⭐ |
Advertencia ética Estas herramientas detectan anomalías, no prueban fraude. Una señal de alarma puede tener explicaciones legítimas:
- Error de transcripción
- Características del instrumento
- Población inusual
- Redondeo por protocolo
Antes de acusar:
- Contactar a los autores
- Buscar explicaciones metodológicas
- Replicar el análisis
- Consultar expertos
Acto III: El veredicto
Después de cinco pruebas forenses, el panorama es claro:
| Prueba | La Prudente | La Entusiasta | La Confiada |
|---|---|---|---|
| Media | ✓ | ✓ | ✓ |
| Variabilidad | ❌ | ❌ | ❌ |
| Último dígito | ❌ | ⚠️ | ❌ |
| Runs test | ❌ | ❌ | ❌ |
| Benford | ❌ | ⚠️ | ❌ |
| TOTAL | 1/5 | 1/5 | 1/5 |
Ceremonia: Los Premios Pinocho 2025
🥇 Pinocho de Oro — Mejor mentirosa
Ganadora: La Entusiasta
Su estrategia de escribir muchos números tuvo un efecto inesperado: al
tener más valores, su distribución fue ligeramente menos sesgada.
“Ganaste no por mentir bien, sino por mentir tanto que algunos errores
se cancelaron.”
🥈 Pinocho de Plata — Creatividad en el error
Ganadora: La Confiada
Su conocimiento de fisiología le permitió acertar la media casi
perfectamente. Pero ese mismo conocimiento la traicionó: estaba TAN
segura del rango “normal” que evitó los extremos con fervor religioso.
“Sabías demasiado para mentir bien.”
🥉 Pinocho de Bronce — Consistencia en el fracaso
Ganadora: La Prudente
Falló en cada prueba de manera predecible. Su aversión al riesgo produjo
el rango más estrecho, la menor variabilidad, y la mayor concentración
de 0s y 5s.
“Tu prudencia te delató. En estadística, lo seguro es sospechoso.”
Por qué esto importa
Este juego usa las mismas técnicas que detectan fraude real:
| Campo | Aplicación |
|---|---|
| Auditoría contable | Facturas inventadas |
| Integridad científica | Datos fabricados en papers |
| Ensayos clínicos | Resultados manipulados |
| Elecciones | Anomalías en conteos |
| Declaraciones fiscales | Ingresos inventados |
En 2012, el psicólogo Diederik Stapel fue descubierto por anomalías estadísticas. En 2011, Marc Hauser de Harvard cayó por patrones imposibles.
La estadística no olvida. Y no perdona.
Epílogo: Las Tres Leyes del Mentiroso Numérico
Después de este experimento, tres verdades quedaron claras:
🥇 Primera Ley: El centro es fácil, los extremos son difíciles
Cualquiera puede adivinar que la hemoglobina promedio está “alrededor de 135”. Pero incluir un 118 o un 153 —valores raros pero reales— requiere valentía estadística que el cerebro fraudulento no tiene.
🥈 Segunda Ley: La aleatoriedad es incómoda
Cuando intentas parecer aleatorio, produces patrones más ordenados que la realidad. Evitas repetir números. Alternas obsesivamente entre altos y bajos. La naturaleza no tiene esas ansiedades.
🥉 Tercera Ley: Los números redondos son una trampa
Tu cerebro ama el 0 y el 5. En 60 segundos de presión, son tus mejores amigos. Pero en la distribución real, son solo 2 de 10 opciones. Tu preferencia te delata.
La próxima vez que revises un paper y los datos te parezcan “demasiado limpios”, recuerda:
Los datos reales son incómodos, impredecibles, y a veces feos.
Si todo se ve perfecto, probablemente alguien lo perfeccionó.
Y si alguna vez te tienta fabricar datos, recuerda a La Prudente, La Entusiasta y La Confiada.
Ellas también creyeron que podían ganar.
La estadística siempre gana.
Recursos adicionales
Herramientas online:
¡Conviértete en Detective de Datos!
No te quedes solo con la teoría. Estas técnicas forenses pueden salvarte de basar tus investigaciones en datos fraudulentos. ¡Ahora es tu turno de aplicarlas!
💬 Tu Experiencia Como Detective
La comunidad crece cuando compartimos casos reales. ¡Me encantaría leerte en los comentarios!
- ¿Has detectado alguna vez datos sospechosos en tus investigaciones o en papers que hayas revisado?
- ¿Qué técnica forense te resultó más útil para validar la autenticidad de los datos?
- Comparte tu caso más intrigante - cómo sospechaste y qué técnica te dio la prueba definitiva.
🕵️ Lleva la Estadística Forense a Tu Próxima Investigación
Suscríbete a bioestadísticaedu y recibe directamente en tu bandebanda de entrada:
- Casos reales de detección de fraude estadístico
- Plantillas de código para las 7 pruebas forenses
- Alertas sobre nuevas técnicas de auditoría de datos
🔎 ¿Necesitas un Ojo Experto?
Si enfrentas:
- Datos sospechosos en tu investigación que necesitan auditoría forense
- Revisión por pares de un artículo con posibles anomalías estadísticas
- Curso de estadística básica con enfoque forense para tu equipo de investigación
Agenda una consultoría personalizada. Juntos podemos auditar tus datos, entrenar tu equipo en detección de fraudes o desarrollar protocolos de control de calidad para tus investigaciones.
Referencias
-
Benford, F. (1938). The Law of Anomalous Numbers. Proceedings of the American Philosophical Society, 78(4), 551–572.
-
Brown, N. J. L., & Heathers, J. A. J. (2017). The GRIM Test: A Simple Technique Detects Numerous Anomalies in the Reporting of Results in Psychology. Social Psychological and Personality Science, 8(4), 363–369. https://doi.org/10.1177/1948550616673876
-
Carlisle, J. B. (2017). Data fabrication and other reasons for non-random sampling in 5087 randomised, controlled trials in anaesthetic and general medical journals. Anaesthesia, 72(8), 944–952. https://doi.org/10.1111/anae.13938
-
Heathers, J. A. J., & Brown, N. J. L. (2019). SPRITE. PsyArXiv. https://psyarxiv.com/9qfr5/
-
Jameson, J. L., Fauci, A. S., Kasper, D. L., Hauser, S. L., Longo, D. L., & Loscalzo, J. (Eds.). (2018). Harrison’s Principles of Internal Medicine (20th ed.). McGraw-Hill Education.
-
Mosimann, J. E., Wiseman, C. V., & Edelman, R. E. (1995). Data fabrication: Can people generate random digits? Accountability in Research, 4(1), 31–55. https://doi.org/10.1080/08989629508573866
-
Nigrini, M. J. (2012). Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection. John Wiley & Sons.
-
Simonsohn, U. (2013). Just Post It: The Lesson from Two Cases of Fabricated Data Detected by Statistics Alone. Psychological Science, 24(10), 1875–1888. https://doi.org/10.1177/0956797613480366
-
Wald, A., & Wolfowitz, J. (1940). On a test whether two samples are from the same population. The Annals of Mathematical Statistics, 11(2), 147–162.